Excel Modeling: Εφαρμόζοντας Γραμμικό Προγραμματισμό στη λήψη επιχειρηματικών αποφάσεων
![]()
Η επίλυση πρακτικών προβλημάτων της επιχείρησής μας, γίνεται εύκολη, με τη χρήση μαθηματικών μοντέλων. Αυτή η διαδικασία ΜΟΝΤΕΛΟΠΟΙΗΣΗΣ περιγράφει με ακρίβεια το πρόβλημα και με τη χρήση κατάλληλων εργαλείων, φτάνει στη λύση, γρήγορα και αξιόπιστα.
Ένα απλό και εύκολο στη χρήση εργαλείο Μοντελοποίησης επιχειρησιακών διεργασιών είναι το EXCEL, με την εφαρμογή του Πρόσθετου SOLVER. Χρησιμοποιώντας τη μεθοδολογία του Γραμμικού Προγραμματισμού, ο SOLVER δίνει λύσεις σε ένα πρόβλημα που αντιμετωπίζουν όλες οι επιχειρήσεις, αυτό της κατανομής των διαθέσιμων πόρων, σε περιβάλλον περιορισμών, με τον πιο αποτελεσματικό και οικονομικά σκόπιμο τρόπο.
Ας λύσουμε ένα πρακτικό πρόβλημα, που αντιμετωπίζει η επιχείρηση Α – ΕΜΠΟΡΙΚΗ. Α.Ε. Η επιχείρηση διαθέτει 3 (τρεις) Αποθήκες, στην Αθήνα, στη Θεσσαλονίκη και στη Λάρισα. Πρέπει να στείλει, σε 3 (τρεις) πελάτες της, εμπορεύματα που διαθέτει στις Αποθήκες της. Το κόστος μεταφοράς, κάθε μονάδας εμπορεύματος, από κάθε Αποθήκη σε κάθε Πελάτη, δίνεται από τον ακόλουθο Πίνακα:
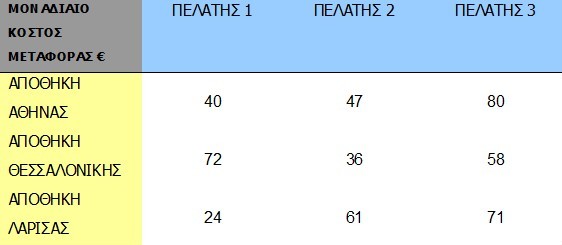
Το πρόβλημα που πρέπει να λύσει η επιχείρηση είναι να βρει πόσα τεμάχια εμπορεύματος πρέπει να στείλει σε κάθε Πελάτη και από ποια Αποθήκη, ώστε το κόστος μεταφοράς να είναι το ελάχιστο δυνατόν.
Οι περιορισμοί του προβλήματος είναι:
- Η χωρητικότητα (διαθεσιμότητα εμπορεύματος) των Αποθηκών
- Η ζήτηση κάθε πελάτη
Γνωρίζοντας τη χωρητικότητα κάθε Αποθήκης, αλλά και τη ζήτηση κάθε Πελάτη, διαμορφώνουμε τον ακόλουθο Πίνακα:
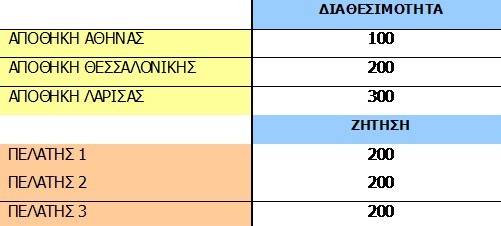
Ας διαμορφώσουμε, τώρα, το μαθηματικό μας μοντέλο.
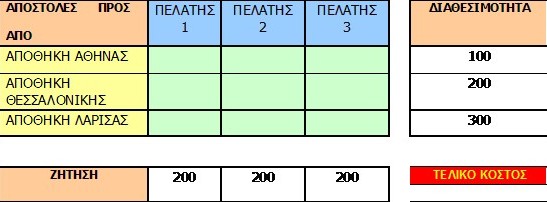
Η πρακτική έννοια των περιορισμών είναι ότι: Το άθροισμα κάθε σειράς, που αντιστοιχεί σε κάθε Αποθήκη, θα πρέπει να είναι μικρότερο ή ίσο με τη διαθεσιμότητα της αντίστοιχης Αποθήκης. Δηλαδή, δεν είναι δυνατόν να διατεθούν, από κάθε Αποθήκη, περισσότερα εμπορεύματα από όσα διαθέτει την παρούσα στιγμή.
Και
Το άθροισμα κάθε στήλης, που αντιστοιχεί σε κάθε Πελάτη, θα πρέπει να είναι μεγαλύτερο ή ίσο με τη ζήτηση του αντίστοιχου Πελάτη. Θα πρέπει, δηλαδή, η αθροιστική διαθεσιμότητα των Αποθηκών σε εμπόρευμα να υπερκαλύπτει τη ζήτηση.
Το συνολικό κόστος κάλυψης της ζήτησης, σε οποιαδήποτε επιλογή που θα κάνει η Διοίκηση της επιχείρησης, θα είναι το σύνολο της επιβάρυνσης που θα υποστεί η επιχείρηση στέλνοντας τις ποσότητες εμπορευμάτων από κάθε Αποθήκη στον αντίστοιχο Πελάτη.
Το ζητούμενο είναι να βρεθούν οι τιμές στα πράσινα τετράγωνα, έτσι ώστε να πληρούνται οι προηγούμενοι περιορισμοί, δηλ. της κάλυψης της ζήτησης των Πελατών από τη δυναμικότητα των Αποθηκών και το κόστος να είναι το ελάχιστο δυνατό.
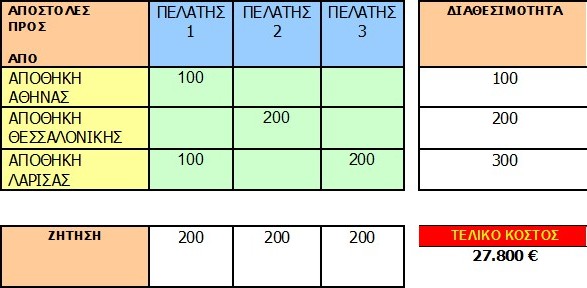
Ας δώσουμε δοκιμαστικές τιμές στα πράσινα τετράγωνα, να δούμε ποιο θα είναι το συνολικό κόστος, όπως φαίνεται στον ακόλουθο Πίνακα:
Βλέπουμε, ότι τηρούνται οι περιορισμοί κάλυψης της Ζήτησης από τη Διαθεσιμότητα.
Το συνολικό κόστος είναι : 100 Χ 40 + 200 Χ 36 + 100 Χ 24 + 200 Χ 71 = 4.000 + 7.200 + 2.400 + 14.200 = 27.800 €
Μπορούμε να διαμορφώνουμε διάφορους συνδυασμούς τιμών, στα Πράσινα τετράγωνα και κάθε συνδυασμός θα μας δίνει και μία νέα λύση, η οποία θα είναι μικρότερη ή μεγαλύτερη από την προηγούμενη. Είναι προφανές, ότι μία τέτοια διαδικασία θα είναι χρονοβόρα και επίπονη, αν γινόταν σε απλό φύλλο το EXCEL, με εισαγωγή τιμών με το χέρι, στα κελιά του Πίνακα του μοντέλου.
Αν εφαρμόσουμε, τώρα τον SOLVER του EXCEL, βρίσκουμε μία πιο καλή λύση. Αν συγκρίνουμε τις τιμές που λάβαμε, κατά την προσπάθειά μας, του προηγούμενου σταδίου της απλής εισαγωγής τιμών, θα βλέπαμε ότι κάθε τιμή του κόστους, θα ήταν μεγαλύτερη από αυτήν που βρήκαμε με τον SOLVER.
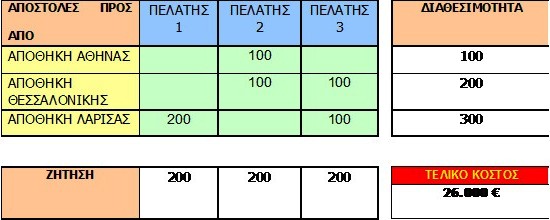
Συνεπώς, η βέλτιστη λύση είναι να σταλούν 200 εμπορεύματα, στον Πελάτη 1 από την Αποθήκη της Λάρισας, 100 εμπορεύματα από την Αποθήκη της Αθήνας και 100 από αυτήν της Θεσσαλονίκης να μεταφερθούν στον Πελάτη 2 και τέλος, 100 εμπορεύματα από την Αποθήκη της Θεσσαλονίκης και άλλα 100 από την Αποθήκη της Λάρισας, να μεταφερθούν στον Πελάτη 3. Το συνολικό κόστος μεταφοράς θα είναι 26.000 €.
Ενεργοποιηθείτε θετικά και επιχειρήστε με προγραμματισμό.
Η ομάδα bizexperts, σας παρέχει μία απλή και εύκολη λύση σε ένα πρακτικό πρόβλημα, συμβάλλοντας ενεργά στη διάδοση της επιστημονικής μεθοδολογίας στις Ελληνικές ΜΜΕ.
Αν επιθυμία σας είναι να εμβαθύνετε περισσότερο, απλά, επικοινωνήστε μαζί μας.









Write a Comment